球面投影
Published:
| 今天在看证明的时候看到一个细节,$d$维球面$S^{d-1}$上均匀分布的点$\mathbf{x}$,向任意一个自然基$\mathbf{e_i}=(0,0,…,1,…,0)$做投影$\mathbf{x}^{\top}\mathbf{e_i}$,问投影绝对值的期望$\mathbb{E}_{\mathbf{x}\sim \mathbf{U}(S^{d-1})}( | \mathbf{x}^{\top}\mathbf{e_i} | )$是多少。 |
| 文章中给出的证明是设$a_i=\mathbb{E}_{\mathbf{x}\sim \mathbf{U}(S^{d-1})}( | \mathbf{x}^{\top}\mathbf{e_i} | )$,由于各向同性$a_1=a_2=\cdots=a_d$,并且 $\sum_i a_i^2=1$ ,所以可以导出$a_i=\frac{1}{\sqrt{d}}$。 |
$a_1=a_2=\cdots=a_d$这个是没什么问题的,但是后一个条件 $\sum_i a_i^2=1$ 我总觉得哪里有点不太对,于是尝试不使用这种整体式条件,直接从$\mathbf{x}^{\top}\mathbf{e_i}$的分布入手来进行思考。
| $\mathbf{x}$在投影前在球面上均匀分布,(我这个傻瓜蛋) 粗略地去想很容易觉得投影之后在对应的坐标轴上也是在$[-1,1]$之间均匀分布,所以绝对值的期望直接就是$\mathbf{E} | \mathbf{U}(-1,1) | =0.5$ |
但是其实这是不对的,拿二维的半圆周(保证$\theta$和$x$一一对应)往$x$轴上投影来说,因为半径$r=1$固定,所以当圆周角$\theta\in\mathbf{U}[0,\pi]$均匀分布时,对应的点也在半圆周上均匀分布,$\theta$的密度函数等于$f_{\theta}=\frac{1}{\pi}$。
借助$x=\cos{\theta},\theta=\arccos{x}$这个关系和密度变换公式, $x$的密度函数为 \(f_{x}=f_{\theta}(x)\cdot |\frac{\partial \theta}{\partial x}|=\frac{1}{\pi}\cdot\frac{1}{\sqrt{1-x^2}}\)
这就表明$x$不是$[-1,1]$上的均匀分布了(密度函数$\frac{1}{2}$)。
既然算都算出来了,顺便就可以把绝对值的期望(半圆)给求一下了。
\[\mathbb{E}_{x\sim f_x}(|x|)=\int_{-1}^{1}|x|\cdot \frac{1}{\pi}\frac{1}{\sqrt{1-x^2}}dx=\frac{2}{\pi}\int_{0}^{1} \frac{x}{\sqrt{1-x^2}}dx=\frac{2}{\pi}\]所以整个圆周投影下来的绝对值的期望就是$\frac{1}{2}\cdot\frac{2}{\pi}\text{(上半圆)}+\frac{1}{2}\cdot\frac{2}{\pi}\text{(下半圆)}=\frac{2}{\pi}\approx 0.6366$
二维的情况是这样,那$d$维的时候又是什么情况呢?
根据stack exchange上的这个回答,我们可以直接跳到一个中间结果 (中间的推导我放到最后了):
$\mathbf{x}^{\top}\mathbf{e}_i$的密度函数正比于$\left(1-t^2\right)^{\frac{d-3}{2}}$
有了密度函数求绝对值的期望就好求了,记规范化常数为$K$,由密度函数积分为1,可以解出K然后代入期望的表达式。
\(\int_{-1}^{1}K\left(1-t^2\right)^{\frac{d-3}{2}}dt=1\) \(\mathbb{E}|\mathbf{x}^{\top}\mathbf{e}_i|=K\int_{-1}^{1}|t|\left(1-t^2\right)^{\frac{d-3}{2}}dt=\frac{2\Gamma(\frac{d}{2})}{(d-1)\sqrt{\pi}\Gamma(\frac{(d-1)}{2})}\)
其实由密度函数的表达式在$d=3$的时候幂次消失,可以看出三维球面是唯一一个投影到坐标轴上得到的是均匀分布的特例,将$d=3$代入绝对值期望的表达式,算出来的值刚好也是0.5,但是$d=2$的时候是0.6366,$d=4$的时候是0.4244,跟均匀分布还是有不小的差距的。
由此我们就解决了第一个问题:均匀分布的$d$维单位球面往自然基上投影绝对值的期望是$\frac{2\Gamma(\frac{d}{2})}{(d-1)\sqrt{\pi}\Gamma(\frac{(d-1)}{2})}$,而不是一开始那样简单粗暴证明出来的$\frac{1}{\sqrt{d}}$。但是有趣的事情还没完,我们可以计算出各个维度的真实期望,把它与$\frac{1}{\sqrt{d}}$做比较,可以得出下面这样一张图:
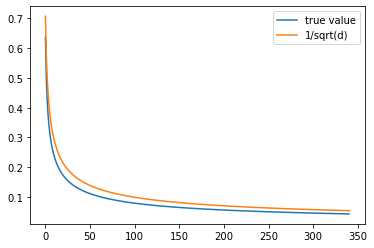
可以看到,我们精心算出来的真实值刚好被前面粗略计算出来的$\frac{1}{\sqrt{d}}$给界住了,那么这一部分怎么证明呢?
我们利用这样一个式子(见《数学分析教程下(常庚哲,史济怀)P396 ),对任意的实数a,
\[\lim_{d\to\infty}\frac{d^a\cdot\Gamma(d)}{\Gamma{(d+a)}}=1\]利用这个式子,可以把原式中的$\frac{\Gamma(\frac{d}{2})}{\Gamma(\frac{d-1}{2})}$近似为$\sqrt{\frac{d}{2}}$。
此时原式变为$\frac{\sqrt{d}}{\sqrt{2\pi}(d-1)}$,令$t=d-1$,则变为$\frac{\sqrt{t+1}}{\sqrt{2\pi t}}\cdot \frac{1}{\sqrt{t}}$。
在$t>1$上有$\sqrt{\frac{t+1}{2\pi t}}<1$, (因为t+1和$2\pi$t的交点在$(0,1)$之间,交点之后都是斜率更大的$2\pi$t更大了),所以整个真实值$<\frac{1}{\sqrt{d}}$。
附录
证明$d$维球面均匀分布的点$\mathbf{x}$,在自然基$\mathbf{e_i}$上的投影的密度函数正比于$\left(1-t^2\right)^{\frac{d-3}{2}}$
首先引入一组随机变量来辅助我们的证明,设$Z=\left(Z_1, \ldots, Z_d\right)^{\top}$ 是一组i.i.d服从$N(0,1)$的随机变量,由于$Z$具有旋转不变性,所以对其进行规范化后落在$d$维单位球面上的随机向量$U=\frac{Z}{|Z|}$就在单位球上均匀分布。所以等价地,我们只需要研究随机向量$U$在自然基$\mathbf{e}_i$上投影 $T_i=\frac{Z_i}{\sqrt{\sum_i Z_i^2}}$的分布。
注意到$T_i^2=\frac{Z_i^2}{\sum_i Z_i^2}$, 由于$Z_i\ i.i.d \sim N(0,1)$,所以有$Z_i^2\sim \chi^2(1),\sum_{i=2}^d Z_i^2\sim \chi^2(d-1)$。
由Beta分布和卡方分布的关系:如果$X\sim\chi^2(\alpha),Y\sim\chi^2(\alpha)$,则$\frac{X}{X+Y}\sim \operatorname{Beta}\left(\frac{\alpha}{2}, \frac{\beta}{2}\right)$可得
$T_i^2\sim\operatorname{Beta}\left(\frac{1}{2}, \frac{d-1}{2}\right)$,所以对应的密度函数正比例于$(t^2)^{-\frac{1}{2}}(1-t^2)^{\frac{d-3}{2}}$
再次使用密度变换公式,乘上一个$\frac{d t^2}{d t}=2t$,则可以得到$T_i$的密度函数正比于$(1-t^2)^{\frac{d-3}{2}}$。
