InfoBert:从信息瓶颈视角看对抗学习
Published:
大家好呀,又到周末了,又到可以不用跑代码到处瞎逛逛的时间了。今天我们一起来看一篇文章,发表在ICLR2021的InfoBERT: Improving Robustness of Language Models from An Information Theoretic Perspective。
从摘要的内容来看,这篇文章主要采用了两个基于互信息的正则项来训练模型,一个是信息瓶颈正则项,这一项抑制输入和特征表达的有噪互信息;第二项是一个锚定特征正则项,增加局部稳定特征和全局特征的互信息。文章还提供了一种原则性的方法来从理论上分析和提高语言模型在标准训练和对抗训练中的稳健性。那么我们就一起来看看吧!
首先给不熟悉文本对抗样本的小伙伴们普及一下对抗文本的定义:
给定一个有n个单词的句子$x=\left[x_1 ; x_2 ; \ldots ; x_n\right]$,我们称一个满足如下条件的句子为$\epsilon$有界的对抗样本$x^{\prime}=\left[x_1^{\prime} ; x_2^{\prime} ; \ldots ; x_n^{\prime}\right]$
(1)句子的真实意图没有改变,但是分类器的决策改变了;
(2)对于句子中单词$x_i$的词嵌入$t_i$,有$\left|t_i-t_i^{\prime}\right|_2 \leq \epsilon$对任意$i$成立。
好,接下来我们就来看一下文章是怎么样设计出这两个别出心裁的正则项的。
跟一切想用信息瓶颈来做文章的套路一样,这篇文章也是想要从原始数据X中学到一个中间表示T,能够最大限度地保留原始数据中关于标签Y的信息,同时又能压缩信息复杂度。于是作者提出了下面的最大化目标函数:
\[\mathcal{L}_{\mathrm{IB}}=I(Y ; T)-\beta I(X ; T)\]但是,由于原始的互信息项不好控制的原因,这里作者分别对第一项和第二项选取了下界和上界,来获得关于整个目标函数的下界。因为我们现在的目的是最大化目标函数,所以最大化它的下界,也能达到一样的效果。
\begin{equation} \begin{aligned} (1)&\ I(Y ; T) \geq \int p(y, t) \log q_\psi(y \mid t) d y d t\\(2)&\ I(X ; T) \leq \int p(x, t) \log (p(t \mid x)) d x d t-\int p(x) p(t) \log (p(t \mid x)) d x d t \end{aligned} \end{equation}
跟原始的互信息相比其实就是把log里面的Radon–Nikodym导数换成了条件概率,方便用神经网络来进行逼近。
样本记作$\left{x^{(i)}, y^{(i)}\right}_{i=1}^N$,使用均值来代替积分,我们就有了对目标函数具体可以计算的公式:
\[\hat{\mathcal{L}}_{\mathrm{IB}}=\frac{1}{N} \sum_{i=1}^N\left[\log q_\psi\left(y^{(i)} \mid t^{(i)}\right)\right]-\frac{\beta}{N} \sum_{i=1}^N\left[\log \left(p\left(t^{(i)} \mid x^{(i)}\right)\right)-\frac{1}{N} \sum_{j=1}^N \log \left(p\left(t^{(j)} \mid x^{(i)}\right)\right)\right]\]这里可以稍微注意一下下标,第一项和第二项的第一块积分当中都有一个联合密度,所以这两块对应均值中的样本下标只有一个,用i来做标记;第二项的第二块的积分是个x和t互相独立的分布,所以此时用了两个下标ij来分别标识样本,并且要求两次均值。
| 这里的$q_\psi(y | t)$对应BERT里面的自注意力层以及气候的线性分类头,$p(t | x)$对应BERT里面的嵌入层。 |
由于语言模型中隐藏层的维度都较高,所以直接计算$I(X;T)$成本会比较高,文章选择使用计算每个单词与其嵌入之间的互信息$I(X_i;T_i)$作为替代,称下述目标函数为原信息瓶颈的局部形式:
\[\mathcal{L}_{\mathrm{LIB}}:=I(Y ; T)-n \beta \sum_{i=1}^n I\left(X_i ; T_i\right)\]但是其实我有点好奇,既然已经关于i求和了,为什么还要乘一个n。
文章证明了选取的这种局部形式的目标函数实际上是原目标函数的下界:
\[I(Y ; T)-\beta I(X ; T) \geq I(Y ; T)-n \beta \sum_{i=1}^n I\left(X_i ; T_i\right)\]所以说此时最大化局部目标函数,也能达到最大化原目标函数的同样效果。
如果称目标函数的第一项为任务相关的目标函数的话,第二项可以视作一个信息瓶颈正则项,用以控制隐藏层表达T的复杂度。接下来文章分析了为什么增加这样一项正则项有利于提升模型对对抗样本的鲁棒性。
记对抗样本的原始数据与隐藏表示为$X’$和$T’$,干净样本的原始数据为$X$和$T$,隐藏表示$T$和$T’$都具有有限的支撑$\mathcal{T}$,这一点由于自然语言处理中的单词数是有限的,所以可以保证。文章证明了对抗样本与干净样本隐藏层表示与标签的互信息之差可以被原始样本与隐藏层表示之间的互信息所界住:
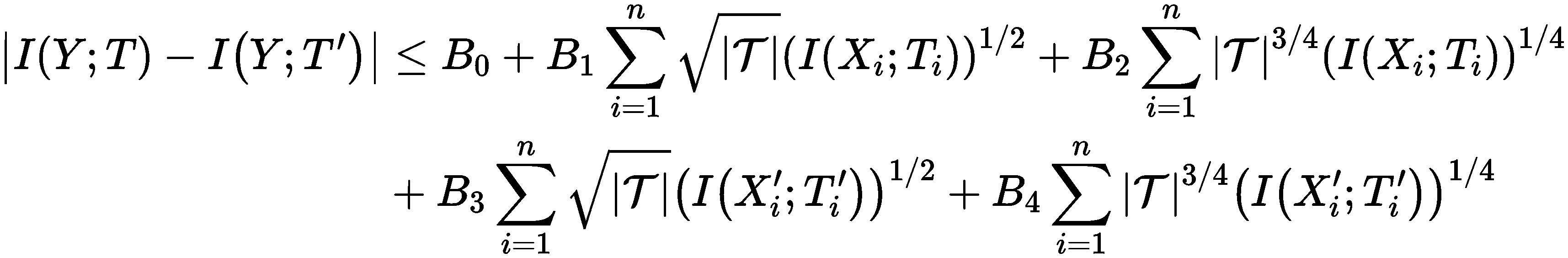
| 右边除去常数项以外主要由四项组成,其中关于干净样本的有两项,关于对抗样本的有两项,唯一的不同仅在于前面关于支撑的势$ | \mathcal{T} | $的次数和互信息本身的次数,一项是二分之一二分之一,另一项是四分之三与四分之一。 |
有了这个关系式,我们就可以看到最小化$I(X_i;T_i)$,以及最小化$I(X_i’;T_i’)$有助于减小模型在干净样本上的表现与在对抗样本上的表现之差。所以使用局部目标函数能够提升模型在对抗数据上的性能就有了理论支撑。
除了这项外,文章还使用了另一个正则项,用于提升局部稳定特征和全局特征的互信息,这又是怎么做的呢?
众所周知,在面对白盒攻击的时候,模型用来做决策的重要关键词句很容易被扰动从而干扰模型的输出。
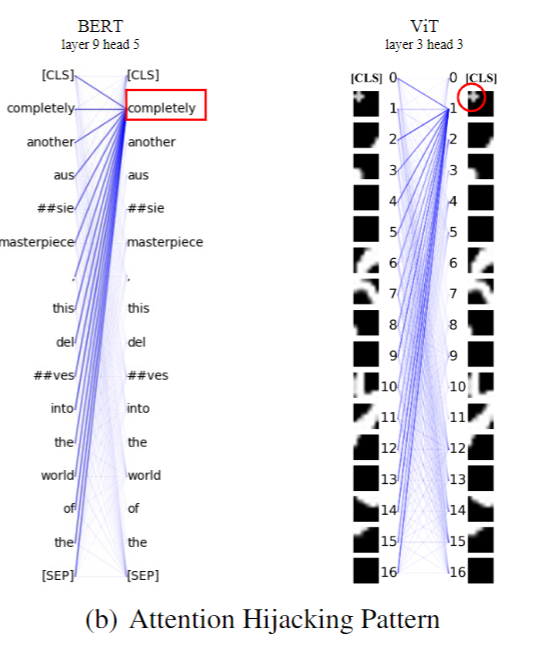
为了提升模型的鲁棒性,作者通过先对模型进行一轮基于梯度的扰动 \begin{equation} \begin{aligned} g(\delta)&=\nabla_\delta \ell_{\text {task }}\left(q_\psi(t+\delta), y\right)\
\delta &\leftarrow \prod_{|\delta|_F \leq \epsilon}\left(\eta g(\delta) /|g(\delta)|_F\right) \end{aligned} \end{equation}
找出那些最容易受到攻击的token(梯度攻击下$\delta$变化幅度最大的)和那些最不容易受到攻击的token(对预测没有贡献多少信息的),留下的变化幅度排名在50%-80%左右的token,视为稳定的特征,然后最大化这些特征与最终放进分类头的[cls] token的互信息,以此来增进另一重的鲁棒性。
\[\max I(Y ; T)-n \beta \sum_{i=1}^n I\left(X_i ; T_i\right)+{\color{blue}\alpha \sum_{j=1}^M I\left(T_{k_j} ; Z\right)}\]这个正则项的设计思路是非常自然的,去掉最容易受到扰动的特征,去掉对决策没什么贡献的特征,把留下来的能对决策做出贡献又不那么容易被扰动的特征拿出来,最大化与[cls] token的互信息,进一步保证了扰动情况下信息量的正常传递,从而能够获得更好的分类准确率。
说完了这个我们可以来看一下实验结果,
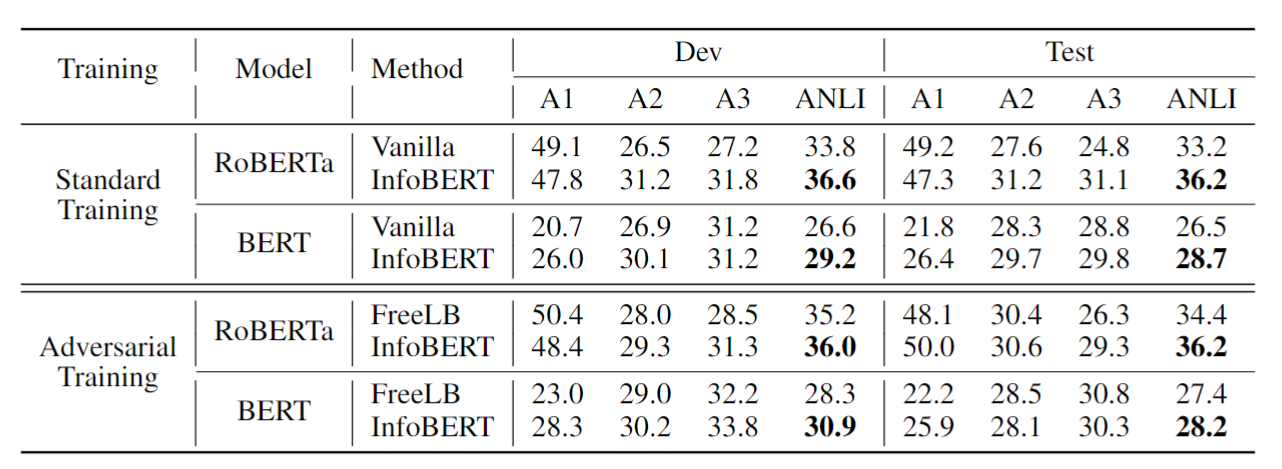
可以看到,比起什么都不加的vanilla模型,增加了两个跟互信息有关正则项的InfoBert可以提升模型在有扰动的数据集ANLI上的准确率1到3个百分点。还有一些别的提升更大的结果,这里由于篇幅所限(加上本人并不太懂NLP)就不一一呈现了,感兴趣的同学可以去看文章。
除了正文里面的主要结果可以看一看以外,相信大家对这两个正则项的消融实验也很感兴趣,他们俩都可以提升效果吗?提升的幅度又如何呢?我们这就一起来看一看:
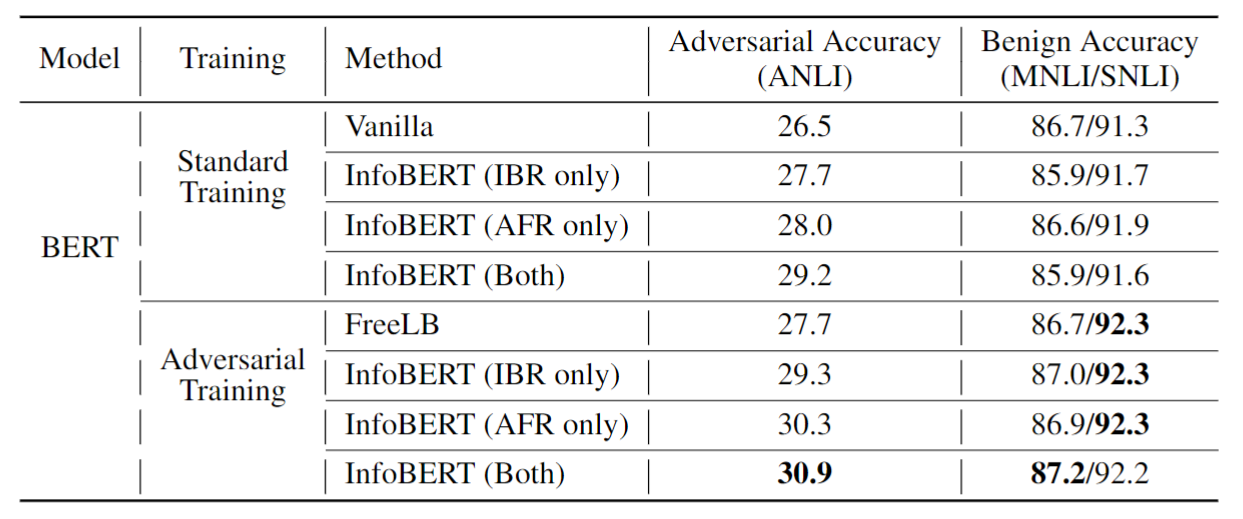
IBR指代所提出的第一个信息瓶颈正则项,AFR指代第二个提出的局部稳定特征正则项。可以看到无论是单独添加还是一起加,模型的对抗准确率都有提升,其中第二项的提升幅度更高一点 。(虽然第一项才是有像模像样理论支持的那个,笑)。
好了,那么到这里我们已经基本明白了文章的大意,接下来我们可以来处理一些之前没太明白的方法论部分的细节:
\[\mathcal{L}_{\mathrm{LIB}}:=I(Y ; T)-n \beta \sum_{i=1}^n I\left(X_i ; T_i\right)\]首先是这个目标函数的具体计算。第一项$I(X;Y)$就直接用最小化cross-entropy loss来代替。那么剩下的就是对正则项的估计。
我们在前面没有进行“局部化”之前是推导过一个原目标函数的估计式的:
\(\hat{\mathcal{L}}_{\mathrm{IB}}=\frac{1}{N} \sum_{i=1}^N\left[\log q_\psi\left(y^{(i)} \mid t^{(i)}\right)\right]-\frac{\beta}{N} \sum_{i=1}^N\left[\log \left(p\left(t^{(i)} \mid x^{(i)}\right)\right)-\frac{1}{N} \sum_{j=1}^N \log \left(p\left(t^{(j)} \mid x^{(i)}\right)\right)\right]\) 现在局部化了之后就先把第二项改为逐个token进行 \(\hat{\mathcal{L}}_{\mathrm{IB}}=\frac{1}{N} \sum_{i=1}^N\left[\log q_\psi\left(y^{(i)} \mid t^{(i)}\right)\right]-\frac{\beta}{N} \sum_{i=1}^N\sum_{k=1}^{n}\left[\log \left(p\left(t_k^{(i)} \mid x_k^{(i)}\right)\right)-\frac{1}{N} \sum_{j=1}^N \log \left(p\left(t_k^{(j)} \mid x_k^{(i)}\right)\right)\right]\)
接下来的焦点就是如何计算$\log \left(p\left(t_k^{(i)} \mid x_k^{(i)}\right)\right)$, 文章采用了一个高斯分布的假设,假设对第k个输入的单词$x_k$,它服从以它的词嵌入为均值,方差固定的一个高斯分布: \(x_k\sim \mathcal{N}\left(t_k, \sigma\right)\)
此时$\log \left(p\left(t_k^{(i)} \mid x_k^{(i)}\right)\right)$就可以写成$\color{blue}-c(\sigma)\left|t_k^{(i)}-t_k^{(i)}\right|_2^2$,其中$c(\sigma)$是$\sigma$相关的常数, $t_k^{(i)}$是从$\mathcal{N}\left(t_k, \sigma\right)$采样出的independent sample,可以通过往$t_k$中添加高斯噪声或者使用$t_k$的对抗样本或者直接就使用$t_k$ ($\sigma=0$)来获取。第二项$p\left(t_k^{(j)} \mid x_k^{(i)}\right)$也对应可以写成$\color{blue}-c(\sigma)\left|t_k^{(i)}-t_k^{(j)}\right|_2^2$,由于这里跨样本进行了相减,所以不需要考虑采样的问题。
class CLUBv2(nn.Module): # CLUB: Mutual Information Contrastive Learning Upper Bound
def __init__(self, x_dim, y_dim, lr=1e-3, beta=0):
super(CLUBv2, self).__init__()
self.hiddensize = y_dim
self.version = 2
self.beta = beta
def mi_est_sample(self, x_samples, y_samples):
sample_size = y_samples.shape[0]
random_index = torch.randint(sample_size, (sample_size,)).long()
positive = torch.zeros_like(y_samples)
negative = - (y_samples - y_samples[random_index]) ** 2 / 2.
upper_bound = (positive.sum(dim=-1) - negative.sum(dim=-1)).mean()
# return upper_bound/2.
return upper_bound
def mi_est(self, x_samples, y_samples): # [nsample, 1]
positive = torch.zeros_like(y_samples)
prediction_1 = y_samples.unsqueeze(1) # [nsample,1,dim]
y_samples_1 = y_samples.unsqueeze(0) # [1,nsample,dim]
negative = - ((y_samples_1 - prediction_1) ** 2).mean(dim=1) / 2. # [nsample, dim]
return (positive.sum(dim=-1) - negative.sum(dim=-1)).mean()
# return (positive.sum(dim = -1) - negative.sum(dim = -1)).mean(), positive.sum(dim = -1).mean(), negative.sum(dim = -1).mean()
def loglikeli(self, x_samples, y_samples):
return 0
def update(self, x_samples, y_samples, steps=None):
# no performance improvement, not enabled
if steps:
beta = self.beta if steps > 1000 else self.beta * steps / 1000 # beta anealing
else:
beta = self.beta
return self.mi_est_sample(x_samples, y_samples) * self.
第一个正则项的计算问题就解决了,那么第二个正则项又怎么计算呢?作者采用了InfoNCE作为互信息的下界来逼近它(又一次): \(\hat{I}^{(\text {InfoNCE })}\left(T_i ; Z\right):=\mathbb{E}_{\mathbb{P}}\left[g_\omega\left(t_i, z\right)-\mathbb{E}_{\tilde{\mathbb{P}}}\left[\log \sum_{t_i^{\prime}} e^{g_\omega\left(t_i^{\prime}, z\right)}\right]\right],\)
其中$g_w$得分函数需要由额外的神经网络来进行逼近,文中选择了两层隐藏层维度为300的MLP来代替;$t_i$表示从局部稳定特征和[cls] token的联合分布中抽出的正样本,$t_i’$表示从不稳定特征与无用特征的联合分布中抽出的负样本。
class InfoNCE(nn.Module):
def __init__(self, x_dim, y_dim):
super(InfoNCE, self).__init__()
self.lower_size = 300
self.F_func = nn.Sequential(nn.Linear(x_dim + y_dim, self.lower_size),
nn.ReLU(),
nn.Linear(self.lower_size, 1),
nn.Softplus())
def forward(self, x_samples, y_samples): # samples have shape [sample_size, dim]
# shuffle and concatenate
sample_size = y_samples.shape[0]
random_index = torch.randint(sample_size, (sample_size,)).long()
x_tile = x_samples.unsqueeze(0).repeat((sample_size, 1, 1))
y_tile = y_samples.unsqueeze(1).repeat((1, sample_size, 1))
T0 = self.F_func(torch.cat([x_samples, y_samples], dim=-1))
T1 = self.F_func(torch.cat([x_tile, y_tile], dim=-1)) # [s_size, s_size, 1]
lower_bound = T0.mean() - (
T1.logsumexp(dim=1).mean() - np.log(sample_size)) # torch.log(T1.exp().mean(dim = 1)).mean()
# compute the negative loss (maximise loss == minimise -loss)
return lower_bound
最后再来看一下文章的大定理
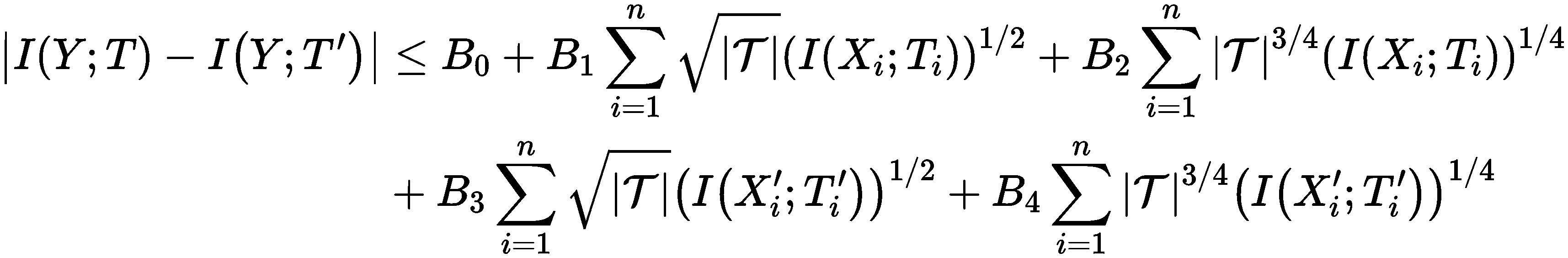
是怎么证明的。
| 证明的关键就是要使用$I(X_i;T_i)$来表示关于Y的互信息差$\left | I(Y ; T)-I\left(Y^{\prime} ; T\right)\right | $。 |
首先我们可以使用互信息的定义将之分成两项:两个条件熵的差与两个熵的差
\[\left|I(Y ; T)-I\left(Y ; T^{\prime}\right)\right| \leq\left|H(T \mid Y)-H\left(T^{\prime} \mid Y\right)\right|+\left|H(T)-H\left(T^{\prime}\right)\right|\]第一项两个条件熵的差可以被下式界住
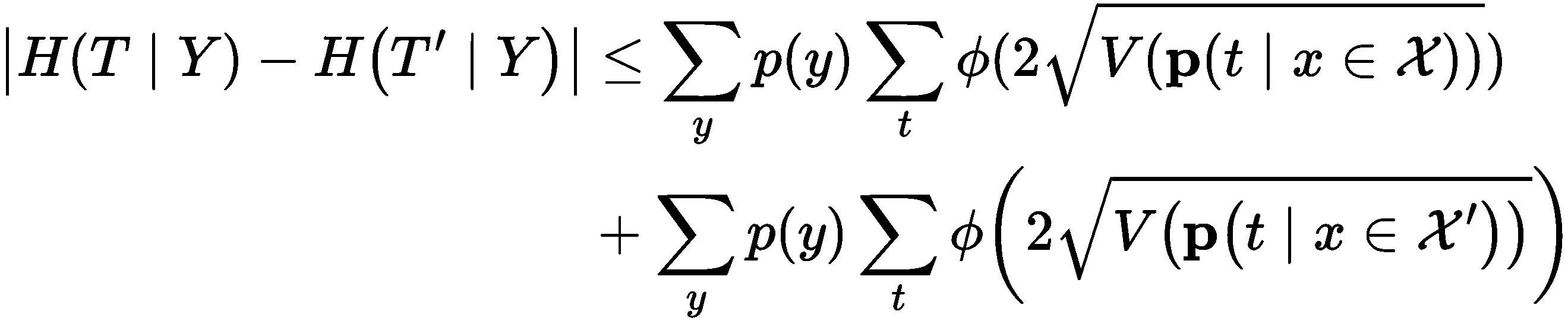
其中$\phi$是一个单调增的次可加函数,V表示方差,$\mathcal{X}$和$\mathcal{X’}$分别表示干净样本与对抗样本的输入空间。经过非常繁琐的推导可以证明

由此即可获得我们最终的bound。
接下来我们再来看一下第二项两个熵之间的差如何界住。首先我们要找到对抗嵌入$T’$与干净嵌入$T$的分布之间的关系。
回顾一开始$\epsilon-$对抗文本的定义,在除了要求对抗文本能骗过分类器外,另一个要求就是对抗文本与干净文本的词嵌入L2距离要小于等于$\epsilon$
\[\left\|t_i^{\prime}-t_i\right\| \leq \epsilon\]利用两种嵌入之间的距离非常接近,我们可以用干净嵌入的分布$p(t)$来定义对抗嵌入的分布$q(t’)$
我们先定义两个量,$Q(t’)$表示对抗嵌入$t’$周围$\epsilon$球中干净嵌入的集合;$c(t)$表示干净嵌入$t$周围$\epsilon$球中对抗嵌入的样本数。我们使用对抗嵌入$t’$周围$\epsilon$球中干净嵌入t的分布来定义对抗嵌入的分布: \(q(t')=\sum_{t\in Q(t')}p(t,t')=\sum_{t\in Q(t')}p(t'|t)p(t)=\sum_{t\in Q(t')}\frac{p(t)}{c(t)}\)
有了这个关系之后,就可以通过计算推导出如下关系式
\[\left|H(T)-H\left(T^{\prime}\right)\right|\leq \left|\sum_t p(t) \log c(t)\right|\]定义$C=\max _t c(t)$,由于语言模型词的数量是有限的,所以该最大值可以取到,由此可以使用常数界住第二项熵的差。
\[\begin{aligned} & \left|H(T)-H\left(T^{\prime}\right)\right| \\ & \leq\left|\sum_t p(t) \log c(t)\right| \\ & \leq\left|\sum_t p(t) \log C\right|=\log C . \end{aligned}\]综合第一项和第二项的界,就可以获得原始的bound。
Encore
还记得为了处理维度过高的问题局部化的时候我问了为什么已经关于单词的维度加起来了还要乘个n吗?这个是为了保证局部化的第二项是原来的一个上界:
\[I(X ; T) \leq n \sum_{i=1}^n I\left(X_i ; T_i\right)\]这样的话我减去局部化的这一项,才能使得整个局部化目标函数是原目标函数的下界,从而最大化局部化目标函数能达到最大化原目标函数的效果。
我们可以一起来证明一下,证明上面这个式子需要先证明一个引理:
引理1: 对于一系列随机变量$X_1,\cdots,X_n$和一个决定性的函数$f$,对任意的$i,j=1,2,\cdots,n$,我们都有
\[I\left(X_i ; f\left(X_i\right)\right) \geq I\left(X_j ; f\left(X_i\right)\right)\]这个引理的意思就是$X_i$与$f(x_i)$的互信息总是比$X_j$与$f(x_i)$的互信息大。这个引理的证明也很直接,利用互信息的定义直接就可以看出来。
证明: 使用互信息与熵和条件熵的关系把两个互信息关于$f(x_i)$进行展开,
\[\begin{aligned} & I\left(X_i ; f\left(X_i\right)\right)=H\left(f\left(X_i\right)\right)-H\left(f\left(X_i\right) \mid X_i\right) \\ & I\left(X_j ; f\left(X_i\right)\right)=H\left(f\left(X_i\right)\right)-H\left(f\left(X_i\right) \mid X_j\right) \end{aligned}\]注意到第一项都是$f(x_i)$的熵,而对于第二项我们有
\[\begin{aligned} & H\left(f\left(X_i\right) \mid X_i\right)=0 \\ & H\left(f\left(X_i\right) \mid X_j\right) \geq 0 \end{aligned}\]所以第一个互信息就等于第一项$f(x_i)$的熵,第二个互信息等于第一项$f(x_i)$的熵再减去一个非零常数,所以第二个互信息小于等于第一个互信息。
有了这个引理我们就可以很方便地证明一开始的上界关系:
记$X=\left[X_1 ; X_2 ; \ldots ; X_n\right]$,$T=\left[T_1 ; T_2 ; \ldots ; T_n\right]=\left[f\left(X_1\right) ; f\left(X_2\right) ; \ldots ; f\left(X_n\right)\right]$,其中$f$是决定性函数。
接下来我们证明
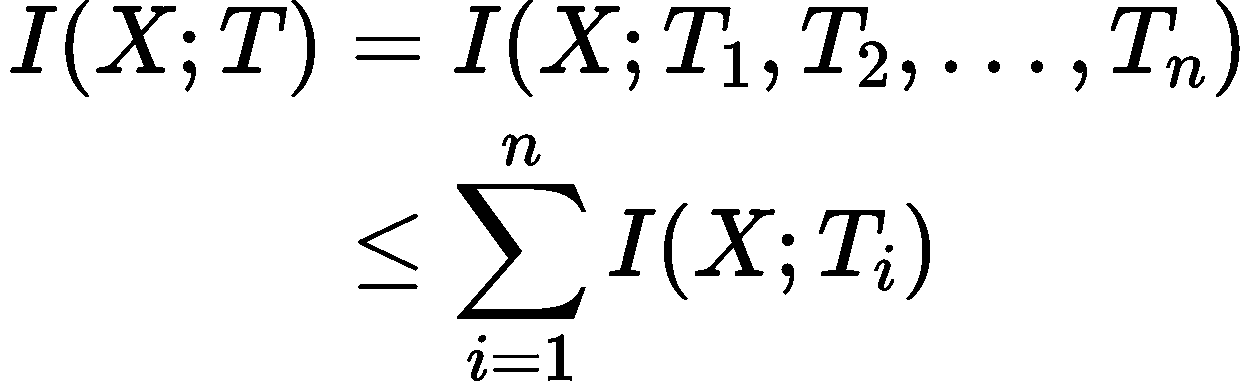
不等号为什么成立,我们可以用一种形象化的方法去看它

这是维基百科Interaction information的一张图,图里每一个圆圈代表这个随机变量完整的熵$H(X)$,$I(X,Y)$就代表两个圆交集的那一块。我们可以以$n=2$为例利用这张图来理解这个不等式为什么成立。假设最上面的圆代表X,左边的圆代表$T_1$,右边的圆代表$T_2$。
可以看到所有圆的公共交集就是我们等式左边的$I(X,T_1,T_2)$,右边求和中的每一项就是除去X之外的每个圆与最上方代表X的圆的交集。因为两个圆之间的交集是肯定包含三个圆的交集的,即右边的每一项都包括了一次等式左边的项,由熵的非负性可知不等式成立。
得到了这个不等式之后我们就可以将X进一步地展开
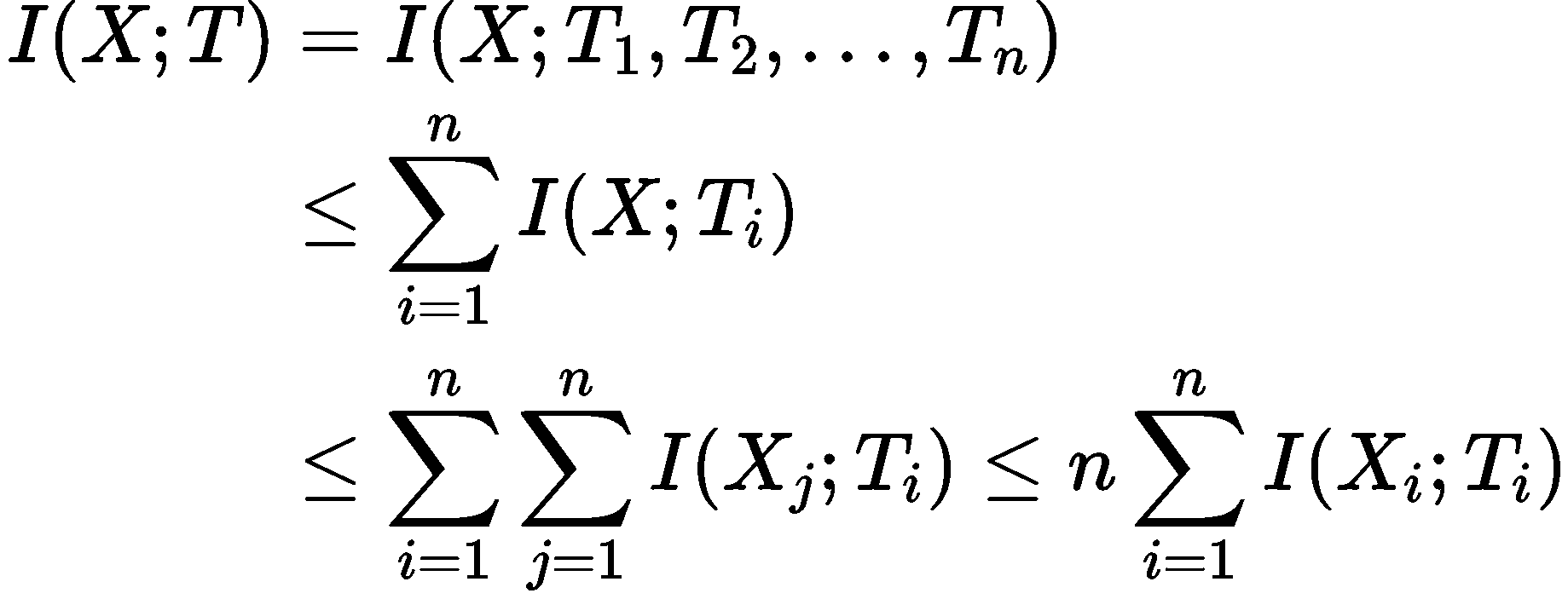
第二个不等号的成立同样是利用了两个圆的交集必然包含所有圆的交集这样一个真理
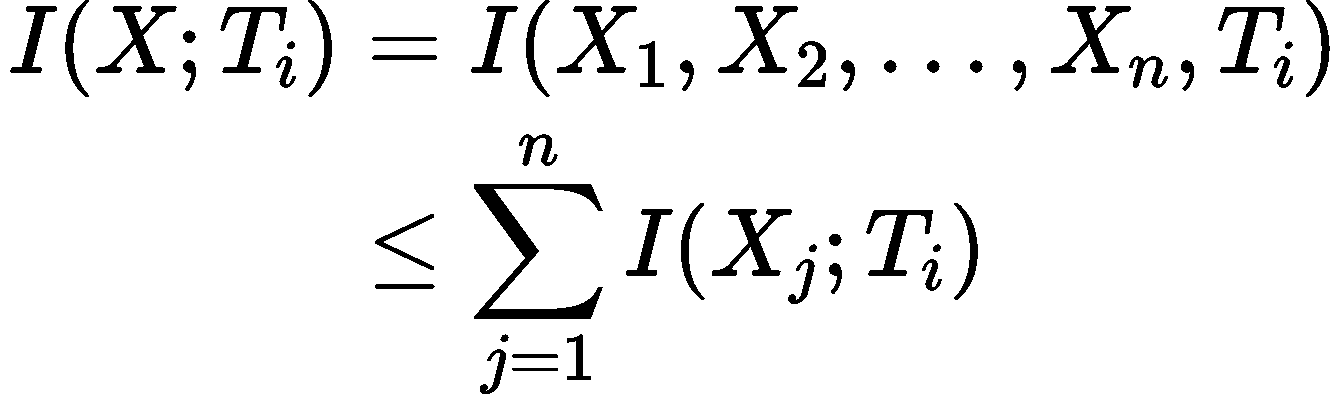
双重求和结合前面证明的引理
$I(X_j,T_i)\leq I(X_i,T_i)$ (因为$T_i=f(X_i)$),
可以把关于j的求和放大变成 \(\sum_{j}I(X_j,T_i)\leq nI(X_i,T_i)\)
由此即获得了我们想要证明的上界,也找出了那个“莫名其妙”的n的来源。
\[I(X ; T) \leq n \sum_{i=1}^n I\left(X_i ; T_i\right)\]好了,今天就到这里吧,祝大家天天开心!(●’◡’●)
